论文信息
**论文:**Recurrent Neural Networks for Multivariate Time Series with Missing Values
**期刊:**Scientific reports 2018
**作者:**Zhengping Che, Sanjay Purushotham, Kyunghyun Cho, David Sontag, Yan Liu
- University of Southern California, Department of Computer Science, Los Angeles, CA, 90089, USA.
- New York University, Department of Computer Science, New York, NY, 10012, USA.
- Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science, Cambridge, MA, 02139, USA. Correspondence and requests for materials should be addressed to Z.C. (email: zche@usc.edu))
Introduction
Abstract
多变量时间序列数据在实际应用中,如卫生保健、地球科学、生物学等,都具有多种缺失值的特征。在时间序列预测和其他相关任务中,已经注意到缺失值及其缺失模式往往与目标标签相关,即**信息缺失。**利用缺失的模式进行有效的估算和提高预测性能方面的工作非常有限。在本文中,我们开发了新的深度学习模型,即grud,作为早期的尝试之一。grud基于门控循环单元(GRU),一种最先进的循环神经网络。它采用缺失模式的两种表示形式,即掩蔽和时间间隔,并将它们有效地整合到一个深入的模型架构中,这样不仅可以捕捉时间序列中的长期时间依赖性,而且还可以利用缺失模式来获得更好的预测结果。在真实世界临床数据集(MIMIC-III, PhysioNet)和合成数据集上进行的时间序列分类任务实验表明,我们的模型实现了最先进的性能,并为更好地理解和利用时间序列分析中的缺失值提供了有用的见解
Motivation
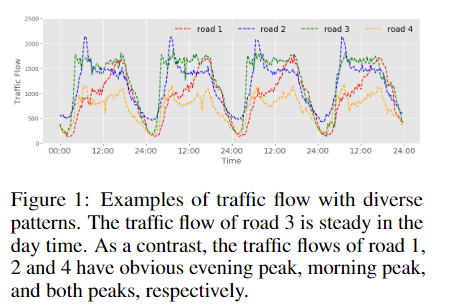
- 由于各种原因,如医疗事故、节省成本、异常情况、不便等,它们往往不可避免地会丢失观测结果。
- 缺失值和模式提供了关于监督学习任务(例如,时间序列分类)中的目标标签的丰富信息。MIMIC-III数据集上信息缺失的演示。下图显示了每个输入变量的缺失率。中间的图是各变量的缺失率与死亡率之间的Pearson相关系数的绝对值。上图为各变量缺失率与ICD-9各诊断类别Pearson相关系数绝对值。观察到缺失率的值与标签相关,低缺失率的变量的缺失率通常与标签高度相关(或正或负)。换句话说,每个患者的变量缺失率是有用的,而这一信息对于数据集中经常观察到的变量更有用
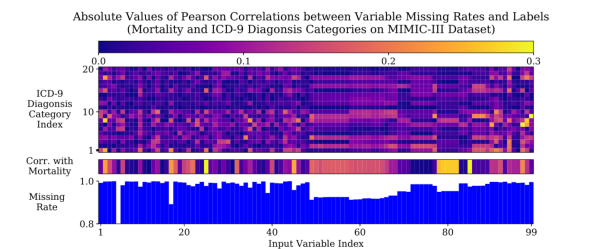
- 现有的一些处理缺失值的办法难以有效解决缺失值的问题:
- **忽略缺失值:**容易造成性能瓶颈
- **数据输入法:(平滑法、插值法和样条法):**不能捕获变量间的相关性和复杂的模式
- **估算方法(光谱分析、核方法、EM算法、矩阵补全和矩阵分解):**推算模型与预测模型分离。这样做,在预测模型中就不能有效地探索缺失的模式,从而导致次优分析结果
- **Main Motivation:**目前还没有针对时间序列分类问题设计融合缺失模式的RNN结构的研究。利用自定义RNN模型的能力以及缺失模式的信息量,是有效建模多元时间序列的一个有前景的新途径
Contribution
- 提出了GRU-D,一个用来处理缺失数据的时间序列的深度学习框架
- 基于masking和time interval提出了识别非完全随机缺失的时间序列的缺失模式的解决方案
- 通过衰减分析研究变量缺失对预测标签的影响。
Method
Notions
多元时间序列:
长度,个变量的时间序列。表示第个时刻的观测值,表示第个时刻的第个变量
时间戳
表示第t次观测时的时间戳,我们假设第一次观测是在时间戳0处进行的
masking vector
表示第个时间步的第个变量是否被观测
时间间隔
表示第个时间步的第个变量上一次观测的间隔
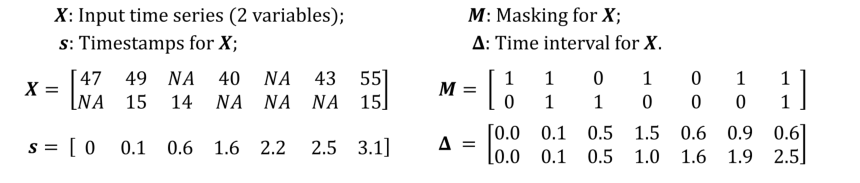
problem
给定标签,
数据:
GRU-RNN for time series classification
有三种直接的方法可以处理缺失的值
- 平均值(GRU-Mean)
(如果缺失,则用平均值$ \tilde{x}^{d}$替代)
- 利用时间结构,假设任何丢失的值与它的最后一次度量相同(GRU-Forward)
(如果缺失,则用上一次取值替代)
- 不明确地输入缺失值,而是通过连接测量、mask和时间间隔向量,简单地指出哪些变量缺失(GRU-Simple)
(不直接给出缺失值)
现有的工作没有同时考虑mask、时间间隔、缺失值输入,对RNN模型结构进行进一步的捕获和利用。
GRU-D: model with trainable decays
衰减
缺失值的重要属性:
- 如果最后观察是很久以前发生的,缺失变量的值趋向于接近一些默认值。这一特性通常作为稳态机制存在于人体的保健数据中,并被认为是疾病诊断和治疗的关键。
- 如果变量丢失了一段时间,输入变量的影响会随着时间的推移而消失。
衰减率:
每个衰减率在0和1之间的合理范围内单调递减
输入衰减
对于一个缺失的变量,使用输入衰减随着时间向经验均值衰减(我们将其作为默认配置),而不是使用最后的观测结果。在此假设下,可训练的衰减方案可以很容易地应用于测量向量。是上一次观测值,是平均值,
隐状态衰减
有时输入衰减可能不能完全捕获丢失的模式,因为不是所有丢失的信息都可以用衰减的输入值来表示
GRU-D
model
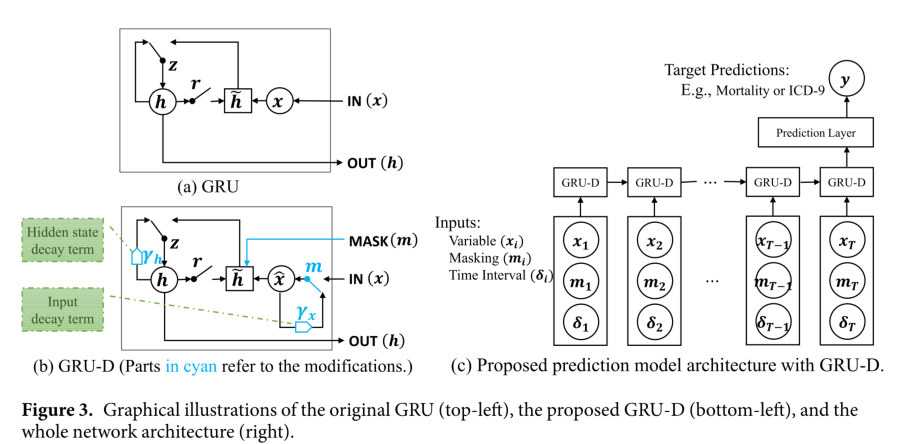
Baseline
解决缺失值分类任务的常见方法是先填充缺失值,然后对输入的数据应用预测模型。这通常需要用额外的运行成本训练额外的模型,并且输入的数据质量不能得到保证。我们的模型避免了依赖于外部的估算方法,但是为了得到公平和完整的比较,我们在实验中测试了几种插值和估算方法,并将它们应用到其他预测基线上。我们包括以下插值和赋值方法:
- Mean, Forward, Simple:三种估算方法,不需要额外训练模型
- SoftImpute:该方法采用迭代软阈值奇异值分解(SVD)矩阵补全法对缺失值进行输入
- KNN:该方法使用k近邻寻找相似样本,通过相似观测值的加权平均计算未观测到的数据
- 三次样条:在该方法中,使用三次样条插值在不同的时间步长的每个特征
- MICE:实践中广泛使用链式方程多重赋值法(MICE),即利用链式方程对不同类型的变量进行多重赋值。
- MF:利用矩阵分解(MF)将不完整矩阵分解成两个低秩矩阵来填补缺失项。
- PCA:利用主成分分析(PCA)模型对缺失值进行赋值
- misforest:这是一种非参数赋值方法,它使用对观测值进行训练的随机森林来预测缺失值
上述三类基线:1. 非RNN基线:LR、SVM、RF。2. RNN类基线,mean、Forward、Simple。 3.GRU-D
基线细节?
Result
Dataset
-
**Gesture phase segmentation dataset (Gesture):**该UCI数据集具有多变量时间序列特征,有规律地采样,没有缺失值,针对5种不同的手势。我们提取378个时间序列并生成4个合成数据集,以了解不同缺失模式下的模型行为。我们将其视为多类分类任务。
-
**PhysioNet Challenge 2012 dataset (PhysioNet):**该数据集来自PhysioNet Challenge 2012,是一个公开的、从8000个重症监护病房(ICU)记录中收集的多变量临床时间序列。每个记录是一个大约48小时的多变量时间序列,包含33个变量,如白蛋白、心率、葡萄糖等。对该数据集进行以下两个预测任务:
- 死亡率任务:预测病人是否会在医院死亡。有554例患者有阳性死亡标记。把它当作一个二元分类问题。
- 所有4个任务:预测4个任务:住院死亡率、住院时间少于3天、患者是否有心脏疾病、手术后是否恢复。我们将其视为一个多任务分类问题。
- **MIMIC-III dataset (MIMIC-III):**该公共数据集确定了临床护理数据,包括2001年至2012年在贝斯以色列女执事医疗中心收集的超过58,000个住院记录。我们从2008-2012年期间收集的19714份住院记录中提取了99个时间序列特征,该系统目前仍在该医院使用。我们的数据集中只包括入院后48小时内仍存活的患者,并且只使用他们入院后48小时内的数据。我们选择了四种形式,即输入事件(进入患者的液体,如胰岛素),输出事件(流出患者的液体,如尿液),实验室事件(化验结果,如pH值、血小板计数)和处方事件(医生处方药物,如阿司匹林和氯化钾)。两个任务:
-
死亡率任务:预测病人在48小时后是否会死于医院。有1716名患者有阳性死亡率标签,我们进行二分类。
-
ICD-9任务:预测20个ICD-9诊断类别(如呼吸系统诊断),作为一个多任务分类问题。
-
利用合成数据集上的信息缺失
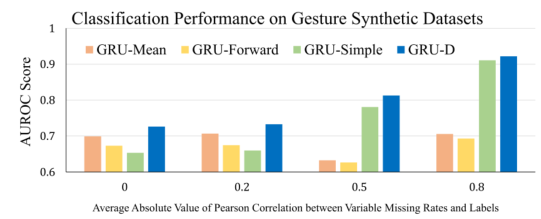
显示了三种GRU基线模型(GRU- mean、GRU- forward、GRU- simple)与提出的GRU- d的AUC得分比较。首先,grug - mean和grug - forward没有利用任何确实(即掩蔽或时间间隔),并在所有4个设置中执行类似的操作。grud - simple和grud受益于对缺失的利用,因此当相关性增加时,它们的性能会更好。它们在具有最高相关性的数据集上实现了相似且最佳的性能。然而,当相关性较低或不存在时,简单地输入缺失表示可能会引入不相关的信息。如图4所示,当相关性较低时,grug - simple失效。另一方面,grud性能稳定,在所有设置中AUC得分最高。这些实证结果验证了我们的假设,即grud仅在相关性较高时使用缺失模式,而在标签和缺失率之间的相关性较低时依赖于观测值。此外,这些合成数据集上的结果表明grud可以正确地建模缺失的模式,并且不引入任何不存在的关系。
对真实数据集的死亡率预测任务评估
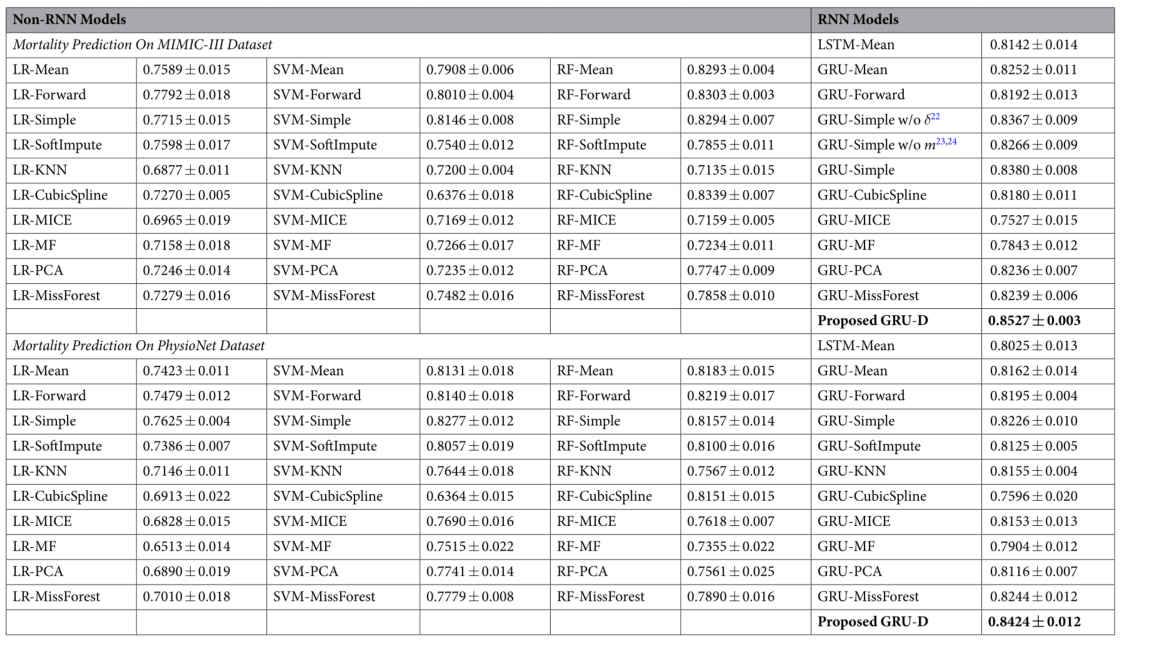
- 除了随机森林之外的所有预测模型在将缺失指标与输入连接起来时表现出了更好的性能
- 两步估计预测方法并没有提高这两个数据集的预测性能,在很多情况下,这些方法的预测效果更差(GRU-MICE、GRU-MF比GRU-MEAN差)
在真实数据集上的多任务预测
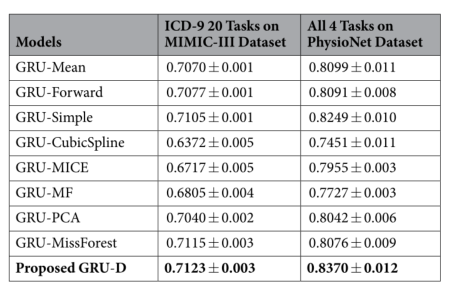
- grud最好