Multi-Horizon TimeSeries Forecasting with Temporal Attention Learning

论文信息

论文：Multi-Horizon TimeSeries Forecasting with Temporal Attention Learning

会议：KDD 2019

作者：

Introduction

时间序列预测问题是研究如何在历史观测的基础上准确地预测未来。提高预测精度有利于提高社会各方面的运行效率

摘要

本文提出了一种新颖的数据驱动方法来解决多水平概率预测任务，该任务可预测未来时间范围内时间序列的完整分布。本文说明，历史信息中隐藏的时间模式在长时间序列的准确预测中起着重要作用。传统的方法依赖于人工建立时间依赖关系来探索历史数据的相关模式，这在现实世界数据的长期序列预测中是不现实的。相反，本文提出显示地学习用深层神经网络构建隐藏模式表征，并关注历史的不同部分来预测未来。

本文提出了一个用于多水平时间序列预测的端到端深度学习的框架，通过时间注意机制，以更好地捕捉历史数据中的潜在模式。基于学习到的潜在模式特征，可以同时生成多个未来水平的多分位数的预测。本文还提出了一种多模式融合机制，该机制用于组合历史不同部分的特征以更好地预测未来。实验结果表明，本文的方法在两个不同领域的大型预测数据集上均实现了最先进的性能。

Motivation

长期预测给基于LSTM的模型带来了挑战（局部动态来源于历史信息和未来的动态输入变量）
有时需要预测目标的总体分布，以帮助企业决策。(分位数预测：一个典型的例子是，库存计划需要对产品的销售进行不同程度的高估，以降低库存缺货成本。根据每种产品的受欢迎程度和缺货成本，从预测分布中选择不同的高估水平)

分位数回归

分位数回归：分位数回归提出的原因，就是因为不希望仅仅是研究y的期望，而是希望能探索y的完整分布状况，

ex1:

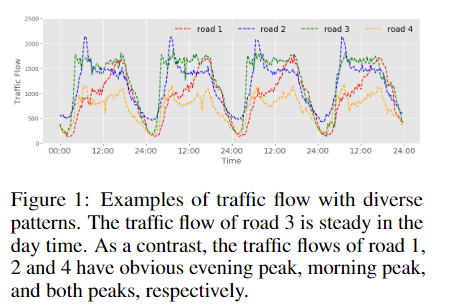
具有分位数预测的现实世界在线销售数据上的销售预测示例。显示了每月50,000种产品的平均日销售量。考虑到洋红色线条所示的2018年1月至3月的历史每日销售额，任务是预测4月至6月。黑线表示实际销售额；深蓝色线表示分位数为0.5的预测；蓝色阴影区域显示分位数预测为0.2和0.8。

Contribution

提出了一种用于多水平时间序列预测的端到端深度学习框架，该框架具有新颖的结构以更好地捕捉未来水平上的时间模式，能组合历史不同部分的特征以更好地预测未来，同时生成多分位数预测。

这个想法是首先使用双向LSTM解码器在向前和向后两个方向上传播未来输入变量的信息，同时考虑诸如促销和日历事件之类的动态未来信息。然后在每个未来的时间步中，我们使用解码器隐藏状态关注历史的几个不同时期，并分别生成关注向量。我们将不同的历史时期视为不同的模式，通过学习每种模式在预测当前时间步长的相对重要性，我们将它们结合起来。组合特征，我们称为时间背景特征，结合历史信息和未来的背景信息，可以最好地描述当前的时间步

Method

Basic encoder-decoder structure

本文采用这个序列到序列的学习流水线来编码历史(和未来)的输入变量，并对未来的预测进行解码

LSTM：将历史信息映射进潜在表示 $h_{t-1}$ : $h_{t}^{e}=L S T M^{e}\left(x_{t} ; h_{t-1}\right)$

$\begin{aligned} i_{t} &=\sigma\left(W_{i x} x_{t}+W_{i m} m_{t-1}\right) \\ f_{t} &=\sigma\left(W_{f x} x_{t}+W_{f m} m_{t-1}\right) \\ o_{t} &=\sigma\left(W_{o x} x_{t}+W_{o m} m_{t-1}\right) \\ c_{t} &=f_{t} \cdot c_{t-1}+i_{t} \cdot \tanh \left(W_{c x} x_{t}+W_{c m} m_{t-1}\right) \\ h_{t} &=o_{t} \cdot \tanh \left(c_{t}\right) \end{aligned}$

$x_{t}$ 为t时刻的输入， $h_{t}$ 为t时刻的隐藏状态

BiLSTM

$\begin{aligned} h_{t}^{f} &=L S T M^{f}\left(x_{t} ; h_{t-1}\right) \\ h_{t}^{b} &=L S T M^{b}\left(x_{t} ; h_{t+1}\right) \\ h_{t} &=\left[h_{t}^{f} ; h_{t}^{b}\right] \end{aligned}$

quantile predictions

分位数的预测（K维）

$\begin{aligned} y_{t}^{e} &=W_{e} h_{t}^{e}+b_{e} \\ y_{t}^{d} &=W_{d} h_{t}^{d}+b_{d} \end{aligned}$

Structure

分为Encoder 和Decoder
Encoder 编码历史信息，使用单向的LSTM对历史信息进行编码
Decoder使用编码的历史信息作为初始状态，使用未来信息作为输入，生成未来序列的输出，采用的是双向的LSTM（使未来的每个时间片都能得到未来和过去的输入信息。）
最后的预测应该在BiLSTM中信息传播之后进行，换句话说，并不使用之前时间步的预测结果来预测当前的时间步。将信息传播阶段与预测阶段分离的目的是为了防止误差积累，特别是对于长水平预测

Attention

由于LSTM记忆机制，需要不断的擦除旧的记忆，更新新的观测值，所以很难捕捉长程依赖。可以使用基于位置的注意力模型(position-based attention model)来捕捉历史数据中的伪周期模式。但是，他们的模型存在误差积累问题，同时需要动态的未来信息，这对预测精度有很大的影响。而且，他们的模型很难直接应用于长时间的历史，因为他们的注意力适用于整个历史，可能会被明显稀释

Stracture

Temporal attention

在译码阶段，在每个未来时间步上使用BiLSTM hidden state来关注历史的不同部分，从而形成未来步的隐藏表示。没有关注整个历史，（1. 历史数据可能非常长， 2. 分别关注不同的时期，与多模态可以结合起来捕获周期信息）

公式：

$\begin{array}{l}\mathrm{g}=\mathrm{v}_{g}^{\top} \tanh \left(\mathrm{W}_{g} \mathrm{~s}_{t}+\mathrm{V}_{g} \mathrm{~h}+\mathrm{b}_{g}\right) \\ \gamma_{i}=\frac{\exp \left(g_{i}\right)}{\sum_{j=1}^{T_{h}} \exp \left(g_{j}\right)} \quad \text { for } i=1 \ldots T_{h}\end{array}$

$\begin{aligned} \mathbf{c}_{t} &=\sum_{i=1}^{T_{h}} \gamma_{i} \mathbf{h}_{i} \\ \mathbf{d}_{t} &=\operatorname{ReLU}\left(\mathbf{W}_{d} \mathbf{c}_{t}+\mathbf{b}_{d}\right) \end{aligned}$

Multimodal fusion

使用之前计算出的转换向量 $\mathrm{d}_{t}^{m}$ 和BiLSTM隐藏状态 $s_t$ 计算不同时间段的权值，进一步进行多模态的融合（这的多模态指的是不同的时期）。

公式：

$\begin{aligned} \mathbf{p}_{t}^{m} &=\mathbf{v}_{p}^{\top} \tanh \left(\mathbf{W}_{p} \mathbf{s}_{t}+\mathbf{V}_{p}^{m} \mathbf{d}_{t}^{m}+\mathbf{b}_{p}\right) \\ \phi_{t}^{m} &=\frac{\exp \left(p_{t}^{m}\right)}{\sum_{k=1}^{M} \exp \left(p_{t}^{k}\right)} \quad \text { for } m=1 \ldots M \end{aligned}$

最终得到：

$\mathbf{x}_{t}=\sum_{m=1}^{M} \phi_{t}^{m} \mathbf{d}_{t}^{m}$

实验

数据集

D50K Online Sales Forecasting

本文从全球在线零售公司JD.com收集了庞大的现实世界在线销售数据集。该数据集包括2014年至2018年在中国6个地区销售的不同产品的每日销售数据的50,000个时间序列。坐着感兴趣的是预测所有需求区域中所有产品感兴趣月份的每日需求量，并且感兴趣的是0.50到0.95的分位数预测

由于必须同时考虑多个因素，例如产品类别，地理区域，促销等，因此销售预测具有挑战性。我们简要介绍可用功能，作为数据集中提供的历史和未来信息：

配送中心id
商品分类
促销活动(促销活动假定是预先计划好的，因此可以作为历史和未来的输入变量)
日历信息（节日等信息）

Loss:

$L^{M A D}=\sum_{i} \sum_{q} \frac{1}{T} \sum_{t}\left[q\left(y_{i t}-\hat{y}_{i t}^{q}\right)^{+}+(1-q)\left(\hat{y}_{i t}^{q}-y_{i t}\right)^{+}\right]$

$i \in\{1,2, \ldots, 50,000\}$ 表示第i条序列

$q \in\{0.5,0.6,0.7,0.8,0.9,0.95\}$ 表示预设的分位数

$t$ 表示预测的未来时间步

GEFCom2014 Electricity Price Forecasting

2014年全球能源预测大赛(GEFCom2014)引入的电价预测任务评估模型。GEFCom2014价格预测数据集包含2011-01- 2013-12-31三年的小时电价。这项任务是在平均分配的12个评估周内提供未来24小时的预测。在此数据集中，基于小时的区域和总电力负荷估算是过去和未来信息中都可以使用的两个时间特征。

Loss

$L^{M A D}=\sum_{q} \frac{1}{T} \sum_{t}\left[q\left(y_{t}-\hat{y}_{t}^{q}\right)^{+}+(1-q)\left(\hat{y}_{t}^{q}-y_{t}\right)^{+}\right]$

实验结果

Baseline

Benchmark ：直接复制历史值作为将来的预测
Gradient-Boosting:梯度提升机，这是一种用于回归和分类问题的经典机器学习方法。
POS-RNN ：这是一种深度学习方法，将基于位置的注意力模型应用于序列的历史，并获得一个历史特征
MQ-RNN：使用LSTM编码器将序列的历史总结为一个隐藏特征，并使用MLP对隐藏特征与所有未来输入变量一起对所有未来范围进行预测，避免了错误累计。
TRMF：通过添加可衡量观察训练时间序列可能性的正则化项，将时间依赖性纳入矩阵分解模型中。本文采用他们选择的参数进行销售预测

Model variants

BiLSTM-Enc-Dec(h=1)，BiLSTM-Enc-Dec(h=3)是上文提到了不包含Attention机制的 LSTM encoder and BiLSTM decoder模型，其中h表示模型编码的历史信息的周期数
Single-Attention(h=1), 只涉及一个历史周期的Attention计算
Multimodal-Attention(h=3)，接受三个时期的历史数据，并首先分别对它们进行多重关注，然后将它们与多模式融合相结合，

Experiment results

分位数损失对比

Benchmark仅仅通过复制历史信息，就达到了 4.98的分位数损失
POS-RNN由于使用attention挖掘历史信息，达到了2.95的分位数损失
MQ-RNN要比POS-RNN更好，它独立输出每个未来的结果，并避免解码阶段的错误累积
bi-lstm - ence - dec (h=1)和bi-lstm - ence - dec (h=3)超出了以前的方法，这多亏了使用BiLSTMdecoder，它可以向前和向后传播动态的未来信息(事件和促销)。
通过结合注意机制，Single-Attention(h=1)模型将bi-lstm模型提高到2.14，而多注意(h=3)模型进一步提高到2.12，该模型使用了三个月的历史数据，并将注意应用于每个月。

MSE对比

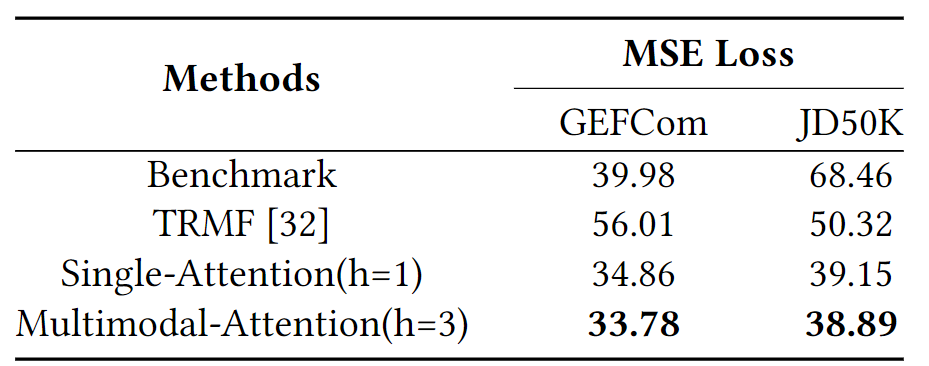
还将在CEFCom2014和JD50K数据集上，将本文的方法Single-Attention（h = 1）和Multimodal-Attention（h = 3）与具有均方误差（MSE）的基准和TRMF [32]进行了比较。所示，在两个数据集上，本文提出的方法总是优于基准和TRMF超过20％，Multimodal-Attention（h = 3）优于Single-Attention（h = 1）约3％