论文 :Disentangling and Unifying Graph Convolutionsfor Skeleton-Based Action Recognition(分解和统一图卷积用于基于骨骼的动作识别)
**会议:**CVPR 2020
作者:
使用时空图的基于骨架的动作识别算法
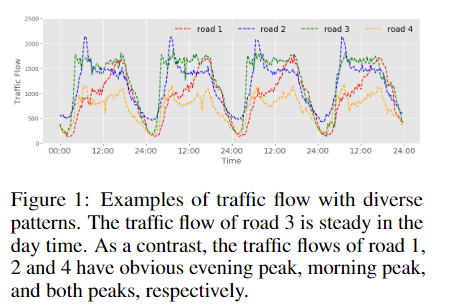
时空图被基于骨架的动作识别算法广泛地用于建模人的动作动力学,为了从这些图中捕获强大的运动模式,远距和多尺度上下文聚合和时空依赖建模是功能强大的特征提取器的关键方面。
现有方法局限,难以实现的方面 :
在多尺度操作下的无偏的远距关节的关系建模
无阻碍的跨时空信息流,捕获复杂的时空不连续
早期工作:
早期基于骨架的动作识别方法将人类关节视为一组独立的特征,它们通过手工制作的或学习的这些特征的聚合来建模空间和时间的关节相关性。这些方法忽略了人体关节之间的内在关系,而以关节为节点、以其自然连通性(即骨头)为边的人体骨骼图最能捕捉关节之间的内在关系。因此,最近的方法(图方法)用骨架时空图来模拟一个动作的关节运动模式,骨架时空图是在不同时间步间携带着空间和时间维度信息的一系列不相连和非对称的骨架图
作者认为:一个理想的骨架识别算法应该超越局部的关节关联,提取多尺度的结构特征和长期的依赖关系,因为结构上分开的关节也可以有很强的相关性
远距离关系捕获:
然而现在的方法都是使用A(邻接矩阵)的k阶幂指数来获得k阶邻居,通过邻接矩阵A的高阶幂来扩大感受野。但是使用幂指数的方式会存在biased weighting problem
biased weighting problem :在求某个节点的k阶邻居时,距离该节点近的和度比较大的权重会比较高。在骨架图上,这意味着较高的多项式阶数只能有效地捕获来自远距关节的信息,因为聚合的特征将由局部身体部位的关节主导
复杂时空关系建模:
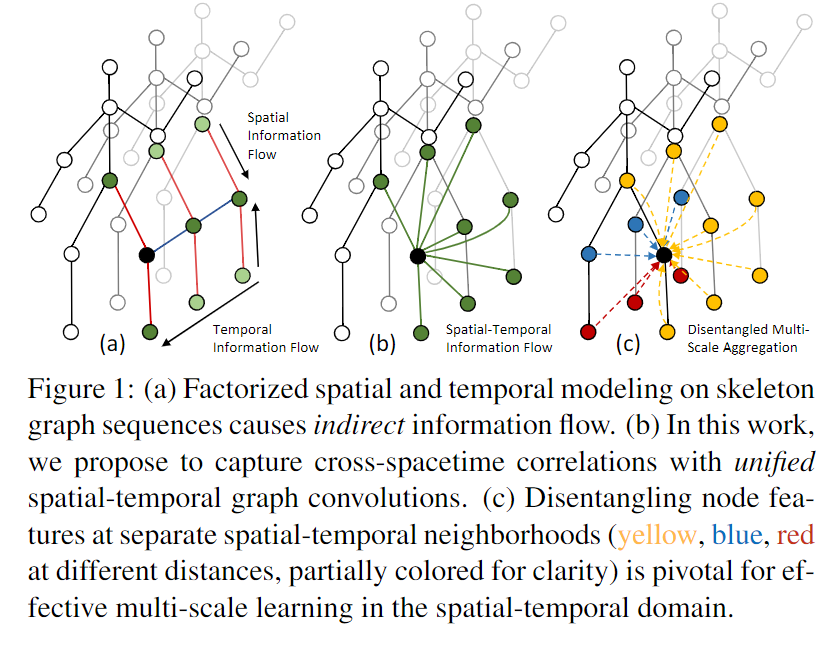
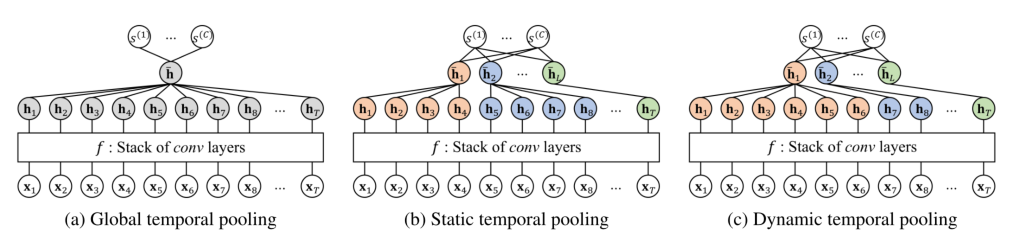
利用复杂的跨时空关节关系进行建模,目前的方法,使用 spatial-only and temporal-only交错的模式,如下图所示。目前比较常用的方法是在每一帧上使用GCN来提取空间信息,在时间上使用TCN或者RNN来进行提取时间信息。虽然这种因式分解(这篇论文中称目前使用的方法为因式分解的方式)的方式允许高效的长时间建模,但它阻碍了跨越时空的直接信息流,从而无法捕捉复杂的区域时空节点。
a)对骨架图序列进行因子化的时空建模会导致间接信息流。 (b)在这项工作中,我们建议使用统一的时空图卷积捕获跨时空相关性。 (c)在不同的时空邻域(黄色,蓝色,不同距离重新划分,为清楚起见,部分着色)分离节点特征对于在时空领域进行有效的多尺度学习至关重要
总结
邻接矩阵幂指数的方式会存在biased weighting problem
建模复杂的时空关系,使用spatial-only and temporal-only交错的模式是低效的
提出一种新的多尺度聚合方案,通过消除距离较近和距离较远的邻域节点之间的冗余依赖关系来解决有偏加权问题,使得有效的多尺度聚合器有效地捕获人类骨架上的图范围关节关系,不需要考虑节点间的距离
提出了G3D,这是一个新的统一的时空图卷积模块,它直接模拟了跨时空的联合依赖关系。G3D通过在三维时空域内导入图边,作为通畅的时空信息流的跳过连接(图1(b))来实现这一点,极大地促进了时空特征学习,之前的工作只有时间信息流、空间信息流
将解缠结的聚合方案与G3D集成在一起,可提供功能强大的特征提取器(MS-G3D),该提取器具有跨空间和时间维度的多尺度接收场。 时空中特征的直接多尺度聚合进一步提高了模型性能
spectral GNN and spatial
频谱gnn在图的傅里叶域中用一组学习过的滤波器对输入图信号进行滤波。然而,由于特征分解的要求和邻接固定的假设,它们在计算效率和推广新图方面是有限的
空间gnn通常通过以下方式对每个节点进行分层更新:1)选择具有邻域功能的邻域(如相邻节点);(2)使用聚合函数(如聚合函数)合并来自所选邻居和自身的特性。意思是池);以及(3)用激活的转换操作来合并特征(MLP)。
Multi-Scale Graph Convolutions
研究者还提出了多尺度空间GNN来捕获来自非本地邻居的特征。 [1,19,21,45,24]使用图邻接矩阵的高阶多项式来聚合来自远程邻居节点的特征。
早期方法:关注手工制作的特征和下游分类器的联合关系
该领域图卷积的早期应用是ST-GCN,其中空间图卷积和交叉时间卷积用于时空建模
AS-GCN ,2s-AGCN,STGR
G = ( V , E ) \begin{array}{l}\mathcal{G}= (\mathcal{V}, \mathcal{E}) \end{array} G = ( V , E )
其中:
V = { v 1 , … , v N } \mathcal{V}=\left\{v_{1}, \ldots, v_{N}\right\} V = { v 1 , … , v N }
E \mathcal{E} E A ∈ R N × N , A i , j = 1 if an edge directs from v i to v j and 0 \mathbf{A} \in \mathbb{R}^{N \times N},\mathbf{A}_{i, j}=1 \text { if an edge directs from } v_{i} \text { to } v_{j} \text { and } 0 A ∈ R N × N , A i , j = 1 if an edge directs from v i to v j and 0 A A A G \mathcal{G} G
X = { x t , n ∈ R C ∣ t , n ∈ Z , 1 ≤ t ≤ T , 1 ≤ n ≤ N } \begin{array}{l} \mathcal{X}=\left\{x_{t, n} \in \mathbb{R}^{C} | t, n \in\right. \mathbb{Z}, 1 \leq t \leq T, 1 \leq n \leq N\}\end{array} X = { x t , n ∈ R C ∣ t , n ∈ Z , 1 ≤ t ≤ T , 1 ≤ n ≤ N }
$ \begin{array} \mathbf{X} \in \mathbb{R}^{T \times N \times C}, \text { where } x_{t, n}=\mathbf{X}_{t, n,:} \end{array}, , ,
X t ∈ R N × C \mathbf{X}_{t} \in \mathbb{R}^{N \times C} X t ∈ R N × C Θ ( l ) ∈ R C l × C l + 1 \Theta^{(l)} \in \mathbb{R}^{C_{l} \times C_{l+1}} Θ ( l ) ∈ R C l × C l + 1 l l l
t时刻的骨架图上的图卷积公式
X t ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 X t ( l ) Θ ( l ) ) \mathbf{X}_{t}^{(l+1)}=\sigma\left(\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X}_{t}^{(l)} \Theta^{(l)}\right) X t ( l + 1 ) = σ ( D ~ − 2 1 A ~ D ~ − 2 1 X t ( l ) Θ ( l ) )
σ ( ⋅ ) \sigma(\cdot) σ ( ⋅ )
A ~ = A + I \tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I} A ~ = A + I
Disentangled Multi-Scale Aggregation(解纠缠的多尺度聚合):
使用邻接矩阵A A A
X t ( l + 1 ) = σ ( ∑ k = 0 K A ^ k X t ( l ) Θ ( k ) ( l ) ) \mathbf{X}_{t}^{(l+1)}=\sigma\left(\sum_{k=0}^{K} \widehat{\mathbf{A}}^{k} \mathbf{X}_{t}^{(l)} \Theta_{(k)}^{(l)}\right) X t ( l + 1 ) = σ ( ∑ k = 0 K A k X t ( l ) Θ ( k ) ( l ) )
其中l l l K K K
A ^ \widehat{\mathbf{A}} A A A A
对称归一化图拉普拉斯算子:A ^ = L n o r m = I − D − 1 2 A D − 1 2 \widehat{\mathbf{A}}=\mathbf{L}^{\mathrm{norm}}=\mathbf{I}-\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} A = L n o r m = I − D − 2 1 A D − 2 1
随机游走的标准化:A ^ = D − 1 A \widehat{\mathbf{A}} = D^{-1} A A = D − 1 A
GCN(kipf)中的标准化方法:A ^ = D ~ − 1 2 A ~ D ~ − 1 2 \widehat{\mathbf{A}}=\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} A = D ~ − 2 1 A ~ D ~ − 2 1
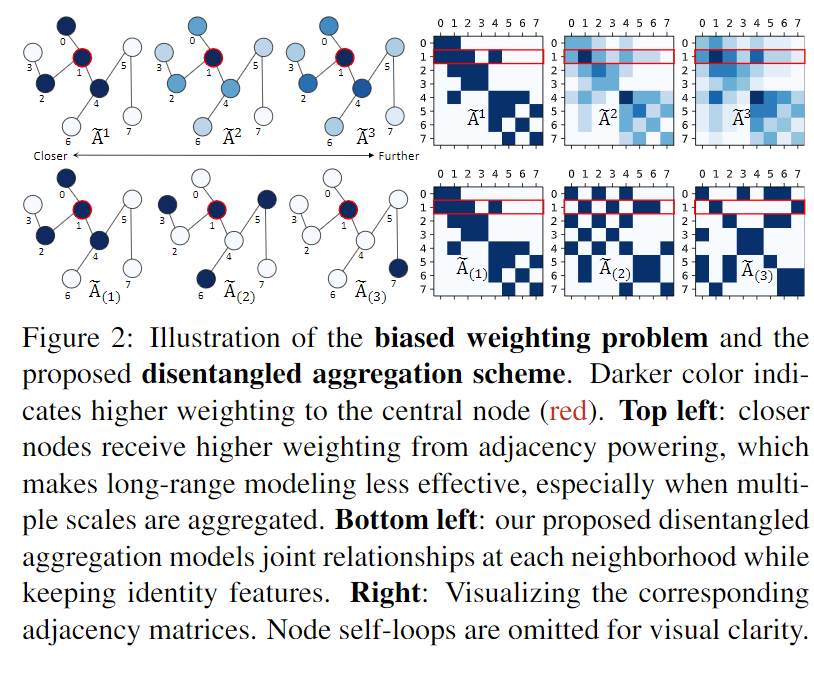
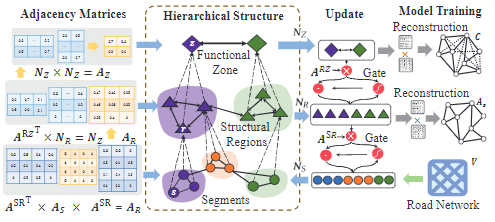
上图说明有偏加权问题和提出的解纠缠聚合方案,颜色越深,表示对中心节点的权重越大(红色)
**TOP-Left:**近距离节点从邻接电源获得更高的权重,这使得远程建模效率较低,特别是当多尺度被聚合时
**Bottom-left:**本文所提出的分离聚集模型在保持特征的同时,在每个邻域处建立联合关系
**Right:**可视化相应邻接矩阵。为了视觉上的清晰,省略了节点自循环
[ A ~ ( k ) ] i , j = { 1 if d ( v i , v j ) = k 1 if i = j 0 otherwise \left[\tilde{\mathbf{A}}_{(k)}\right]_{i, j}=\left\{\begin{array}{ll}1 & \text { if } d\left(v_{i}, v_{j}\right)=k \\ 1 & \text { if } i=j \\ 0 & \text { otherwise }\end{array}\right. [ A ~ ( k ) ] i , j = ⎩ ⎨ ⎧ 1 1 0 if d ( v i , v j ) = k if i = j otherwise
A ~ ( 1 ) = A ~ and A ~ ( 0 ) = I \tilde{\mathbf{A}}_{(1)}=\tilde{\mathbf{A}} \text { and } \tilde{\mathbf{A}}_{(0)}=\mathbf{I} A ~ ( 1 ) = A ~ and A ~ ( 0 ) = I
对于k>1,具体的解除纠缠方法是使用做差
A ~ ( k ) = I + 1 ( A ~ k ≥ 1 ) − 1 ( A ~ k − 1 ≥ 1 ) \tilde{\mathbf{A}}_{(k)}=\mathbf{I}+\mathbb{1}\left(\tilde{\mathbf{A}}^{k} \geq 1\right)-\mathbb{1}\left(\tilde{\mathbf{A}}^{k-1} \geq 1\right) A ~ ( k ) = I + 1 ( A ~ k ≥ 1 ) − 1 ( A ~ k − 1 ≥ 1 ) 1 ( A ~ k ≥ 1 ) 1\left(\tilde{\mathbf{A}}^{k} \geq 1\right) 1 ( A ~ k ≥ 1 )
d ( v i , v j ) d\left(v_{i}, v_{j}\right) d ( v i , v j )
领域解纠缠的具体方法就是第k k k k k k
X t ( l + 1 ) = σ ( ∑ k = 0 K D ~ ( k ) − 1 2 A ~ ( k ) D ~ ( k ) − 1 2 X t ( l ) Θ ( k ) ( l ) ) \mathbf{X}_{t}^{(l+1)}=\sigma\left(\sum_{k=0}^{K} \tilde{\mathbf{D}}_{(k)}^{-\frac{1}{2}} \tilde{\mathbf{A}}_{(k)} \tilde{\mathbf{D}}_{(k)}^{-\frac{1}{2}} \mathbf{X}_{t}^{(l)} \Theta_{(k)}^{(l)}\right) X t ( l + 1 ) = σ ( ∑ k = 0 K D ~ ( k ) − 2 1 A ~ ( k ) D ~ ( k ) − 2 1 X t ( l ) Θ ( k ) ( l ) )
现有的大多数工作都将骨架操作视为一系列不相交图,其中特征通过仅空间(如GCNs)和仅时间(如TCNs)模块提取。作者认为这种因子化的公式对捕获复杂的时空关系是效果不佳的。
本文提出了一种更合理的允许跨空间时间节点连接的方法,这种连接很容易在时空图中形成跨空间时间边
首先定义了一个时间上的滑动窗口τ \tau τ
使用τ \tau τ
G ( τ ) = ( V ( τ ) , E ( τ ) ) \mathcal{G}_{(\tau)}=\left(\mathcal{V}_{(\tau)}, \mathcal{E}_{(\tau)}\right) G ( τ ) = ( V ( τ ) , E ( τ ) )
V ( τ ) = V 1 ∪ … ∪ V τ \mathcal{V}_{(\tau)}=\mathcal{V}_{1} \cup \ldots \cup \mathcal{V}_{\tau} V ( τ ) = V 1 ∪ … ∪ V τ τ \tau τ
计算τ \tau τ A ~ ( τ ) \tilde{\mathbf{A}}_{(\tau)} A ~ ( τ )
A ~ ( τ ) \tilde{\mathbf{A}}_{(\tau)} A ~ ( τ )
A ~ ( τ ) = [ A ~ ⋯ A ~ ⋮ ⋱ ⋮ A ~ ⋯ A ~ ] ∈ R τ N × τ N \tilde{\mathbf{A}}_{(\tau)}=\left[\begin{array}{ccc}\tilde{\mathbf{A}} & \cdots & \tilde{\mathbf{A}} \\ \vdots & \ddots & \vdots \\ \tilde{\mathbf{A}} & \cdots & \tilde{\mathbf{A}}\end{array}\right] \in \mathbb{R}^{\tau N \times \tau N} A ~ ( τ ) = ⎣ ⎢ ⎡ A ~ ⋮ A ~ ⋯ ⋱ ⋯ A ~ ⋮ A ~ ⎦ ⎥ ⎤ ∈ R τ N × τ N
这样建立的邻接矩阵,除了表示原始时刻t的骨架图上的图结构(对角线 ),还引入了不同节点在不同时间上的连接关系,所有的τ \tau τ 除了对角线的其余部分 )
对划分的时空子图进行图卷积运算
X ( τ ) ∈ R T × τ N × C \mathbf{X}_{(\tau)} \in \mathbb{R}^{T \times \tau N \times C} X ( τ ) ∈ R T × τ N × C τ \tau τ τ \tau τ
[ X ( τ ) ( l + 1 ) ] t = σ ( D ~ ( τ ) − 1 2 A ~ ( τ ) D ~ ( τ ) − 1 2 [ X ( τ ) ( l ) ] t Θ ( l ) ) \left[\mathbf{X}_{(\tau)}^{(l+1)}\right]_{t}=\sigma\left(\tilde{\mathbf{D}}_{(\tau)}^{-\frac{1}{2}} \tilde{\mathbf{A}}_{(\tau)} \tilde{\mathbf{D}}_{(\tau)}^{-\frac{1}{2}}\left[\mathbf{X}_{(\tau)}^{(l)}\right]_{t} \Theta^{(l)}\right) [ X ( τ ) ( l + 1 ) ] t = σ ( D ~ ( τ ) − 2 1 A ~ ( τ ) D ~ ( τ ) − 2 1 [ X ( τ ) ( l ) ] t Θ ( l ) )
(实际上依旧需要逐帧进行图卷积运算,但是作者将每一时刻的骨架图节点拓展成周围τ \tau τ
Dilated Windows
采用类似CNN中的空洞卷积的思想,在帧的采样时,设定一个步长d d d d d d
X ( τ , d ) ∈ R T × τ N × C \mathbf{X}_{(\tau, d)} \in \mathbb{R}^{T \times \tau N \times C} X ( τ , d ) ∈ R T × τ N × C
Multi-Scale G3D
将之前多尺度解纠缠的设计加入,得到完整的MS-G3D模型
[ X ( τ ) ( l + 1 ) ] t = σ ( ∑ k = 0 K D ~ ( τ , k ) − 1 2 A ~ ( τ , k ) D ~ ( τ , k ) − 1 2 [ X ( τ ) ( l ) ] t Θ ( k ) ( l ) ) \left[\mathbf{X}_{(\tau)}^{(l+1)}\right]_{t}=\sigma\left(\sum_{k=0}^{K} \tilde{\mathbf{D}}_{(\tau, k)}^{-\frac{1}{2}} \tilde{\mathbf{A}}_{(\tau, k)} \tilde{\mathbf{D}}_{(\tau, k)}^{-\frac{1}{2}}\left[\mathbf{X}_{(\tau)}^{(l)}\right]_{t} \Theta_{(k)}^{(l)}\right) [ X ( τ ) ( l + 1 ) ] t = σ ( ∑ k = 0 K D ~ ( τ , k ) − 2 1 A ~ ( τ , k ) D ~ ( τ , k ) − 2 1 [ X ( τ ) ( l ) ] t Θ ( k ) ( l ) )
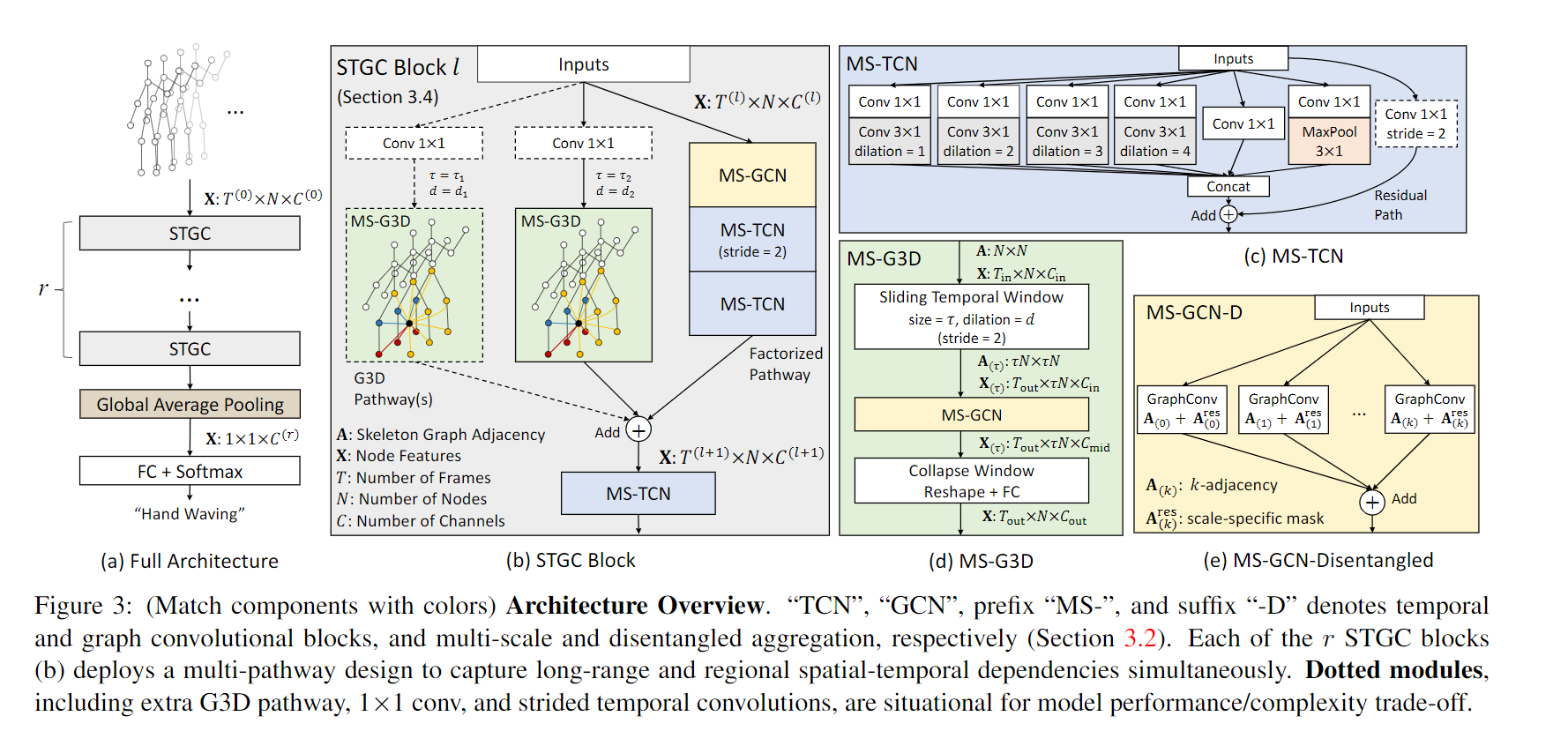
通过堆叠STGC块以从骨架序列中提取特征,再使用全局平均池化和分类器。
STGC主要包含2个部分,以捕获复杂的时空关系
多条MS-G3D路径
将上节提到的MS-G3D设计不同的τ \tau τ d d d
远程、空间和时间模块增强G3D
第一层是多尺度图卷积层(MS-GCN),能够使用最大值K建模整个骨架图
第二第三层是两个多尺度的时间卷积层(MS-TCN,以捕获扩展的时间信息
本文还运用了自适应图的操作
添加一个可学习的、无限制的参数矩阵A r e s \mathbf{A}^{\mathrm{res}} A r e s A ~ ( k ) and A ~ ( τ , k ) \tilde{\mathbf{A}}_{(k)} \text { and } \tilde{\mathbf{A}}_{(\tau, k)} A ~ ( k ) and A ~ ( τ , k )
X t ( l + 1 ) = σ ( ∑ k = 0 K D ~ ( k ) − 1 2 ( A ~ ( k ) + A ( k ) r e s ) D ~ ( k ) − 1 2 X t ( l ) Θ ( k ) ( l ) ) \mathbf{X}_{t}^{(l+1)}=\sigma\left(\sum_{k=0}^{K} \tilde{\mathbf{D}}_{(k)}^{-\frac{1}{2}}\left(\tilde{\mathbf{A}}_{(k)}+\mathbf{A}_{(k)}^{\mathrm{res}}\right) \tilde{\mathbf{D}}_{(k)}^{-\frac{1}{2}} \mathbf{X}_{t}^{(l)} \Theta_{(k)}^{(l)}\right) X t ( l + 1 ) = σ ( ∑ k = 0 K D ~ ( k ) − 2 1 ( A ~ ( k ) + A ( k ) r e s ) D ~ ( k ) − 2 1 X t ( l ) Θ ( k ) ( l ) )
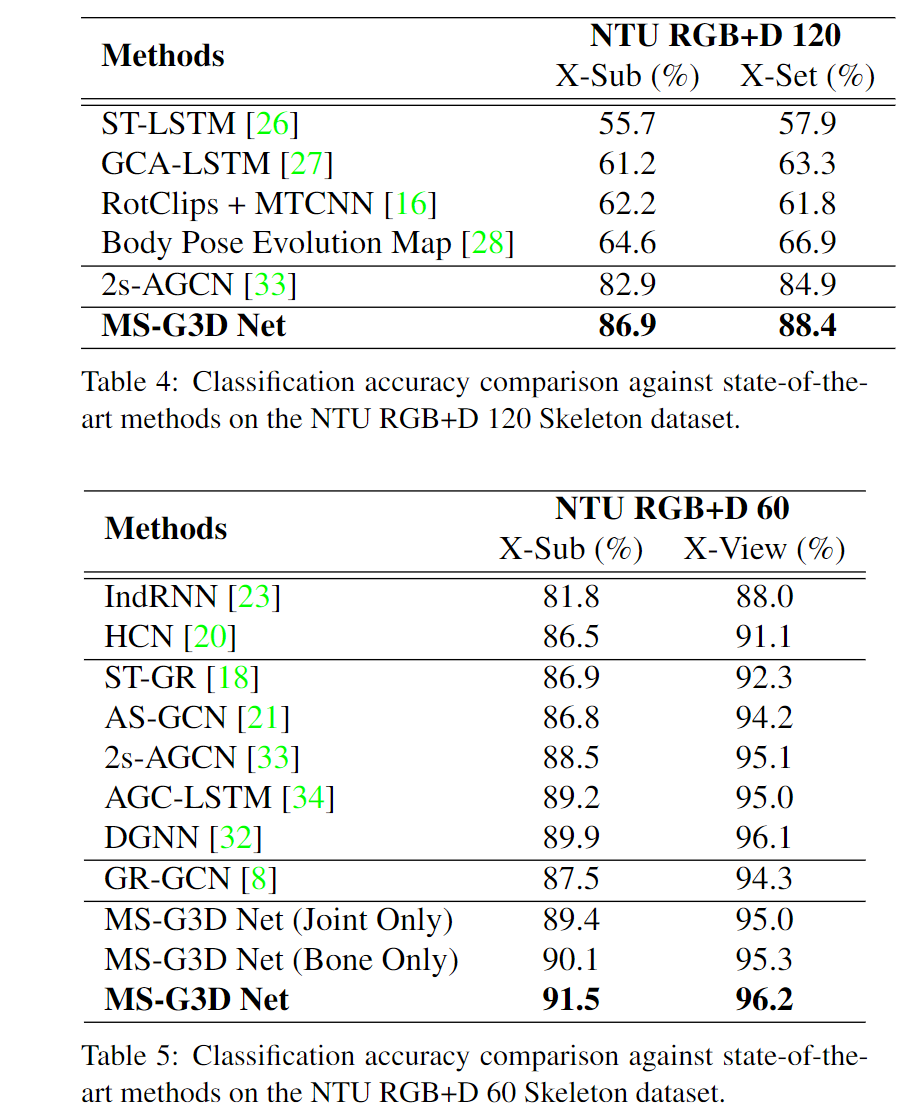
1. NTU RGB+D 60 and NTU RGB+D 120
NTU RGB+D 60:60个动作,25个关节点
NTU RGB+D 120:120个动作,25个关节点
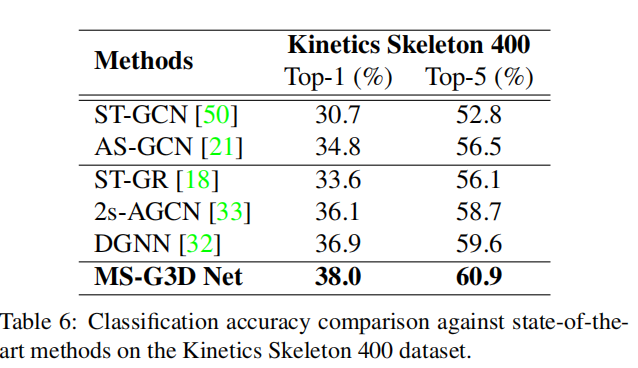
2. Kinetics Skeleton 400
400类,18个关节点
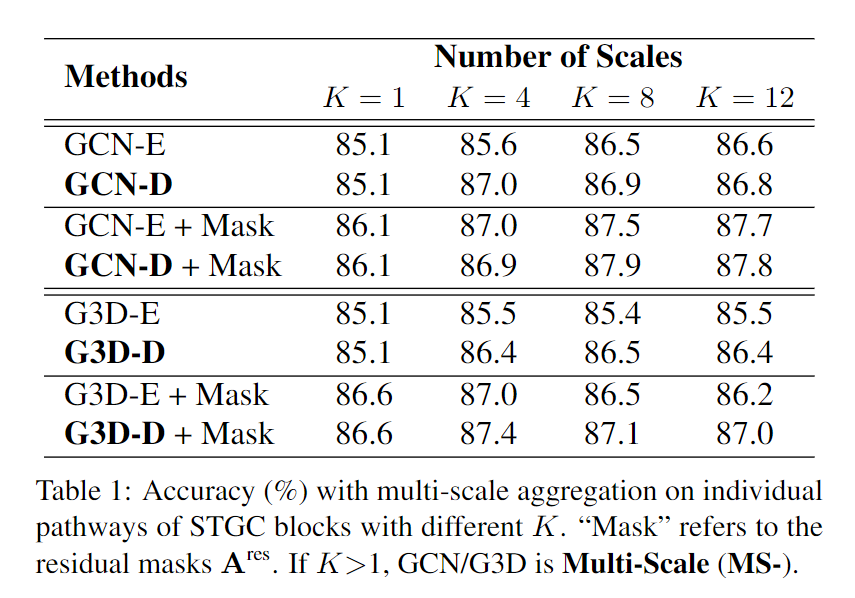
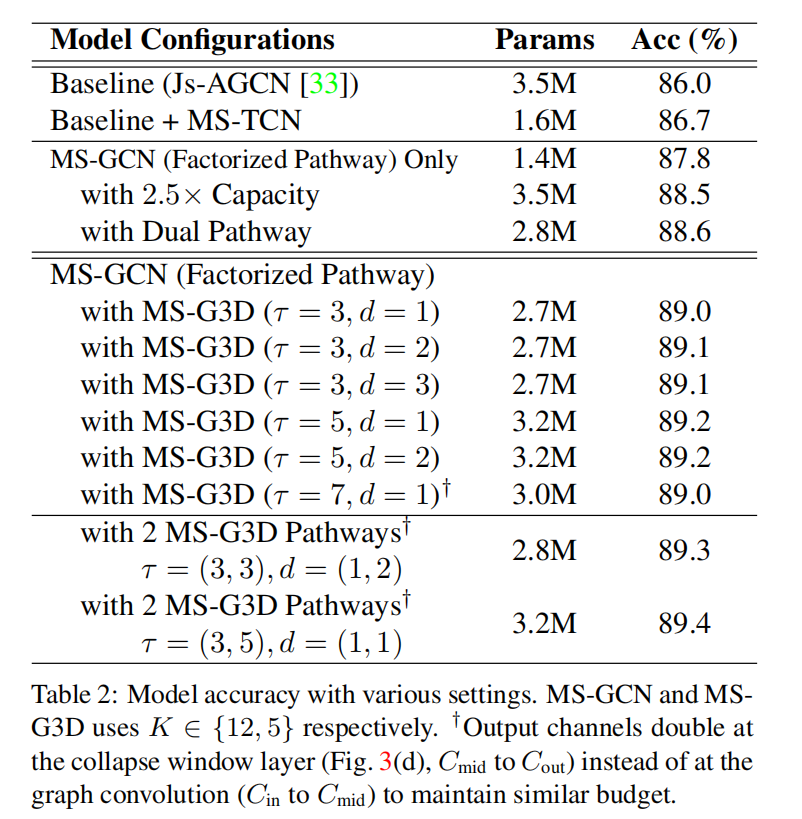
-E表示 adjacency powering,-D表示Disentangling Neighborhoods,mask表示A r e s \mathbf{A}^{\mathrm{res}} A r e s
Disentangling Neighborhoods能带来性能的提升
A r e s \mathbf{A}^{\mathrm{res}} A r e s G3D-E和G3D-D的对比表明,Disentangling Neighborhoods有效解决了biased weighting problem的问题
两条MS-G3D路径能够捕获更复杂的关系
X-Sub指将受试者划分成训练群体和测试群体进行实验
X-view使用固定的camera采集的数据作为测试集,其余的camera采集的数据集作为训练集